Полнофункциональная цифровая фотограмметрическая система.
НОВАЯ версия: 8.1.5504 x64 (загрузить).
Мероприятия
Выставки и конференции
25.09.2025
Завершила работу XXIV Международная конференция «ЦИФРОВАЯ РЕАЛЬНОСТЬ: космические и пространственные данные, технологии обработки».
Конференция была организована АО «Ракурс».
Медиа-партнеры конференции: журнал «Геопрофи», журнал «Информация и Космос», деловое издание и web-портал «НОЗС». Екатеринбург, 22-25 сентября, 2025 г.
Конференция была организована АО «Ракурс».
Медиа-партнеры конференции: журнал «Геопрофи», журнал «Информация и Космос», деловое издание и web-портал «НОЗС». Екатеринбург, 22-25 сентября, 2025 г.
Объявления
Доступны материалы IV Совместной международной научно-технической конференции «ЦИФРОВАЯ РЕАЛЬНОСТЬ: космические и пространственные данные, технологии обработки»
Услуги
- Весь спектр цифровых фотограмметрических работ.
- Многократный контроль на всех технологических этапах.
- Индивидуальный подход к каждому проекту.
- Скорость и качество работ.
- Использование программно-аппаратного обеспечения собственной разработки.
- Предпроектное обследование.
- Разработка технологических решений.
- Сравнительный анализ вариантов.
- Поставка и внедрение разработанных технологических решений.
Технологии
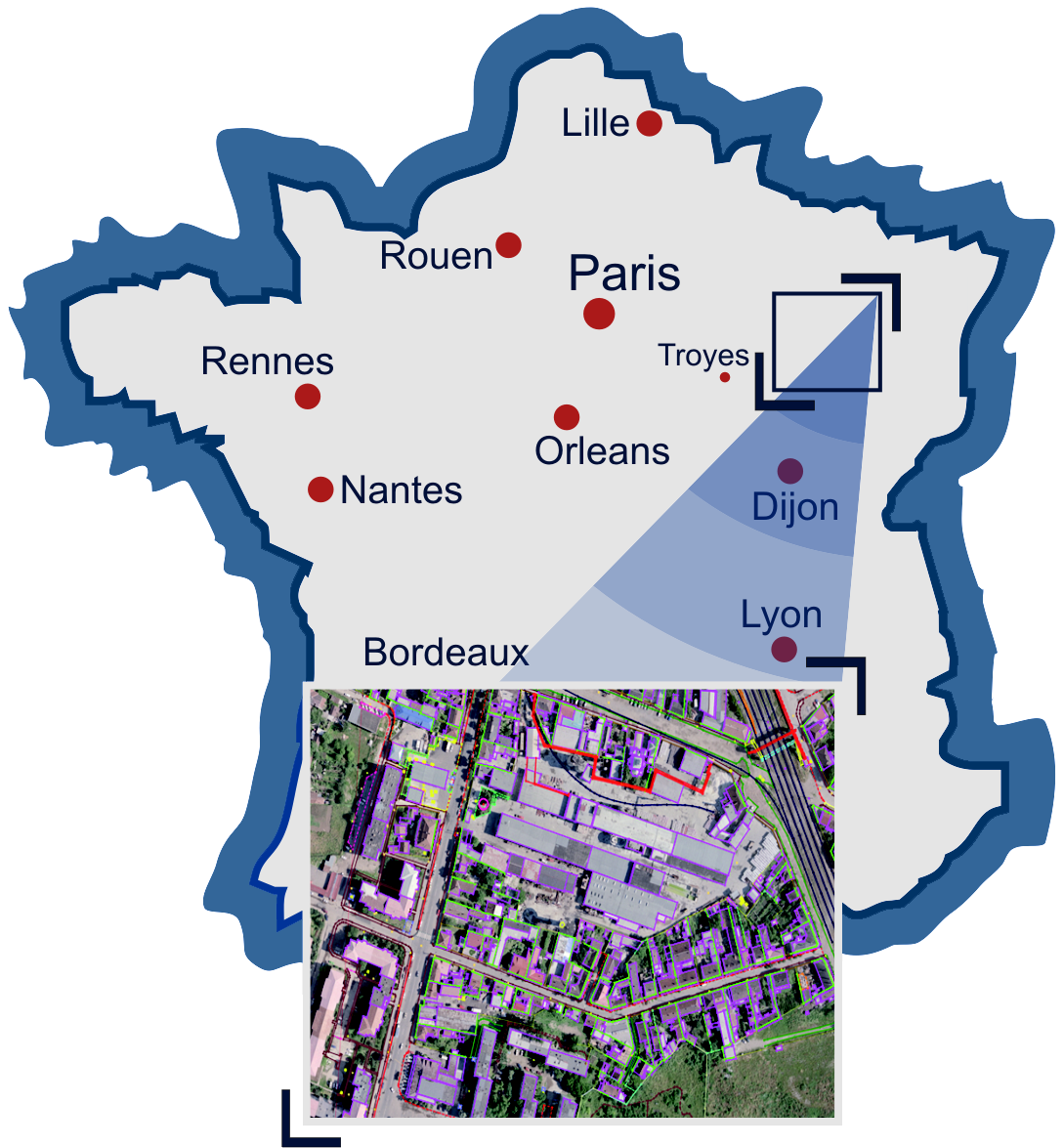
Цель — создание топографической базы данных на территорию Франции.
#топографическая база
#стереовекторизация
#дешифрирование
#топографическая база
#стереовекторизация
#дешифрирование
Использовано ПО:
Результаты:
- Обработано 4,5% территории Франции.
- Классификатор содержал 133 кода.
- Точность векторизации в 3D — 1 м.
- Задействовано 40 операторов.