–ü–æ–ª–Ω–æ—Ñ—É–Ω–∫—Ü–∏–æ–Ω–∞–ª—å–Ω–∞—è —Ü–∏—Ñ—Ä–æ–≤–∞—è —Ñ–æ—Ç–æ–≥—Ä–∞–º–º–µ—Ç—Ä–∏—á–µ—Å–∫–∞—è —Å–∏—Å—Ç–µ–º–∞.
–ù–û–í–ê–Ø –≤–µ—Ä—Å–∏—è: 7.51.4477 x64 (–∑–∞–≥—Ä—É–∑–∏—Ç—å).
–ú–µ—Ä–æ–ø—Ä–∏—è—Ç–∏—è
13 - 16 –Ω–æ—è–±—Ä—è 2023–≥.
–í—ã—Å—Ç–∞–≤–∫–∏ –∏ –∫–æ–Ω—Ñ–µ—Ä–µ–Ω—Ü–∏–∏
06.10.2022
–ò—Ç–æ–≥–∏ 2-–π –°–æ–≤–º–µ—Å—Ç–Ω–æ–π –ú–µ–∂–¥—É–Ω–∞—Ä–æ–¥–Ω–æ–π –Ω–∞—É—á–Ω–æ-—Ç–µ—Ö–Ω–∏—á–µ—Å–∫–æ–π –∫–æ–Ω—Ñ–µ—Ä–µ–Ω—Ü–∏–∏ ¬´–¶–ò–§–Ý–û–í–ê–Ø –Ý–ï–ê–õ–¨–ù–û–°–¢–¨: –∫–æ—Å–º–∏—á–µ—Å–∫–∏–µ –∏ –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–µ–Ω–Ω—ã–µ –¥–∞–Ω–Ω—ã–µ, —Ç–µ—Ö–Ω–æ–ª–æ–≥–∏–∏ –æ–±—Ä–∞–±–æ—Ç–∫–∏¬ª, –°–∞–Ω–∫—Ç-–ü–µ—Ç–µ—Ä–±—É—Ä–≥, 12-15 —Å–µ–Ω—Ç—è–±—Ä—è, 2022 –≥.
–û–±—ä—è–≤–ª–µ–Ω–∏—è
–î–æ—Å—Ç—É–ø–Ω—ã –º–∞—Ç–µ—Ä–∏–∞–ª—ã 2-–π –°–æ–≤–º–µ—Å—Ç–Ω–æ–π –∫–æ–Ω—Ñ–µ—Ä–µ–Ω—Ü–∏–∏ ¬´–¶–ò–§–Ý–û–í–ê–Ø –Ý–ï–ê–õ–¨–ù–û–°–¢–¨: –∫–æ—Å–º–∏—á–µ—Å–∫–∏–µ –∏ –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–µ–Ω–Ω—ã–µ –¥–∞–Ω–Ω—ã–µ, —Ç–µ—Ö–Ω–æ–ª–æ–≥–∏–∏ –æ–±—Ä–∞–±–æ—Ç–∫–∏¬ª
–£—Å–ª—É–≥–∏
- –í–µ—Å—å —Å–ø–µ–∫—Ç—Ä —Ü–∏—Ñ—Ä–æ–≤—ã—Ö —Ñ–æ—Ç–æ–≥—Ä–∞–º–º–µ—Ç—Ä–∏—á–µ—Å–∫–∏—Ö —Ä–∞–±–æ—Ç.
- –ú–Ω–æ–≥–æ–∫—Ä–∞—Ç–Ω—ã–π –∫–æ–Ω—Ç—Ä–æ–ª—å –Ω–∞ –≤—Å–µ—Ö —Ç–µ—Ö–Ω–æ–ª–æ–≥–∏—á–µ—Å–∫–∏—Ö —ç—Ç–∞–ø–∞—Ö.
- –ò–Ω–¥–∏–≤–∏–¥—É–∞–ª—å–Ω—ã–π –ø–æ–¥—Ö–æ–¥ –∫ –∫–∞–∂–¥–æ–º—É –ø—Ä–æ–µ–∫—Ç—É.
- –°–∫–æ—Ä–æ—Å—Ç—å –∏ –∫–∞—á–µ—Å—Ç–≤–æ —Ä–∞–±–æ—Ç.
- –ò—Å–ø–æ–ª—å–∑–æ–≤–∞–Ω–∏–µ –ø—Ä–æ–≥—Ä–∞–º–º–Ω–æ-–∞–ø–ø–∞—Ä–∞—Ç–Ω–æ–≥–æ –æ–±–µ—Å–ø–µ—á–µ–Ω–∏—è —Å–æ–±—Å—Ç–≤–µ–Ω–Ω–æ–π —Ä–∞–∑—Ä–∞–±–æ—Ç–∫–∏.
- –ü—Ä–µ–¥–ø—Ä–æ–µ–∫—Ç–Ω–æ–µ –æ–±—Å–ª–µ–¥–æ–≤–∞–Ω–∏–µ.
- –Ý–∞–∑—Ä–∞–±–æ—Ç–∫–∞ —Ç–µ—Ö–Ω–æ–ª–æ–≥–∏—á–µ—Å–∫–∏—Ö —Ä–µ—à–µ–Ω–∏–π.
- –°—Ä–∞–≤–Ω–∏—Ç–µ–ª—å–Ω—ã–π –∞–Ω–∞–ª–∏–∑ –≤–∞—Ä–∏–∞–Ω—Ç–æ–≤.
- –ü–æ—Å—Ç–∞–≤–∫–∞ –∏ –≤–Ω–µ–¥—Ä–µ–Ω–∏–µ —Ä–∞–∑—Ä–∞–±–æ—Ç–∞–Ω–Ω—ã—Ö —Ç–µ—Ö–Ω–æ–ª–æ–≥–∏—á–µ—Å–∫–∏—Ö —Ä–µ—à–µ–Ω–∏–π.
–¢–µ—Ö–Ω–æ–ª–æ–≥–∏–∏
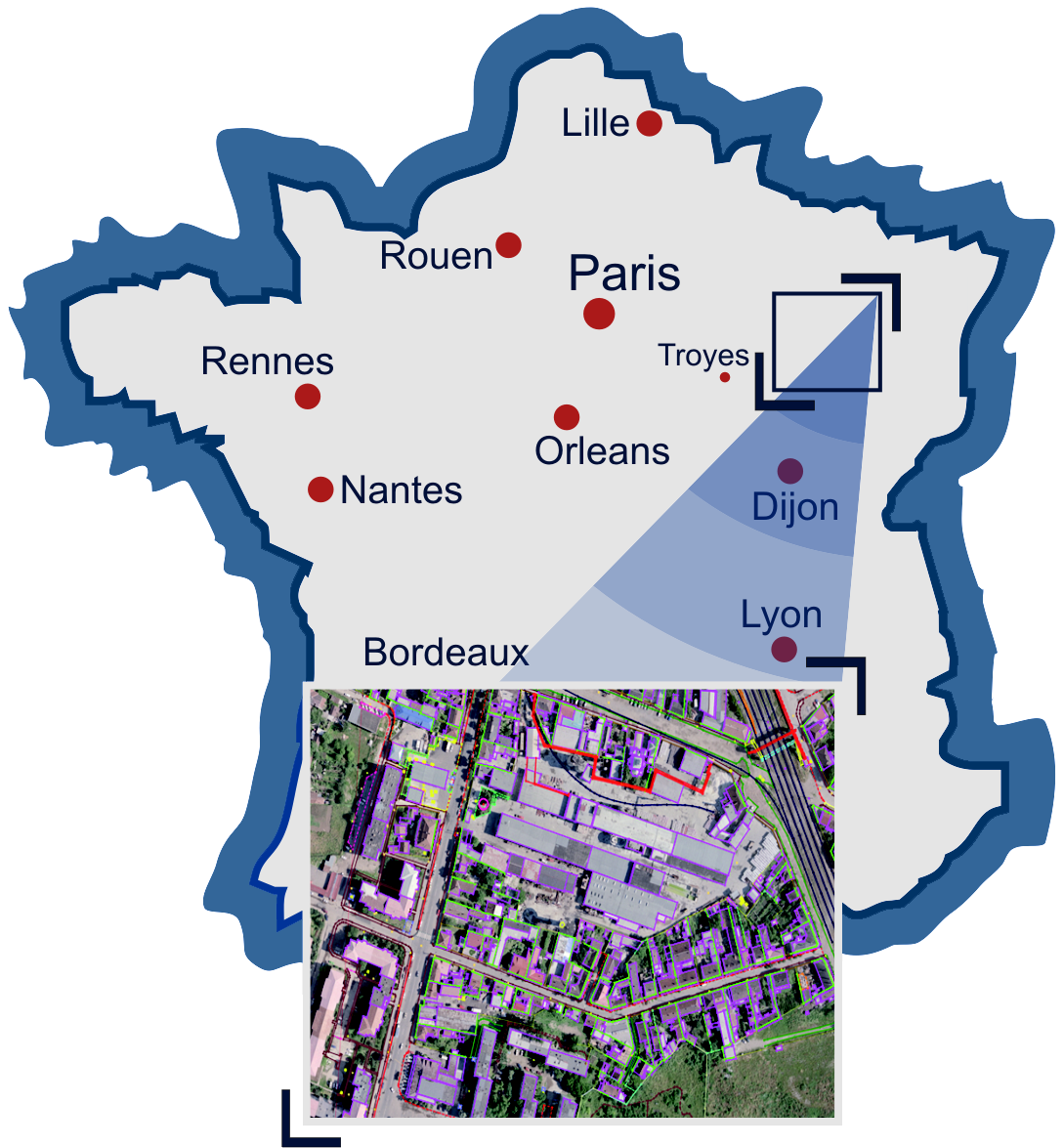
Цель — создание топографической базы данных на территорию Франции
#—Ç–æ–ø–æ–≥—Ä–∞—Ñ–∏—á–µ—Å–∫–∞—è –±–∞–∑–∞
#—Å—Ç–µ—Ä–µ–æ–≤–µ–∫—Ç–æ—Ä–∏–∑–∞—Ü–∏—è
#–¥–µ—à–∏—Ñ—Ä–∏—Ä–æ–≤–∞–Ω–∏–µ
#—Ç–æ–ø–æ–≥—Ä–∞—Ñ–∏—á–µ—Å–∫–∞—è –±–∞–∑–∞
#—Å—Ç–µ—Ä–µ–æ–≤–µ–∫—Ç–æ—Ä–∏–∑–∞—Ü–∏—è
#–¥–µ—à–∏—Ñ—Ä–∏—Ä–æ–≤–∞–Ω–∏–µ
–ò—Å–ø–æ–ª—å–∑–æ–≤–∞–Ω–æ –ü–û:
–Ý–µ–∑—É–ª—å—Ç–∞—Ç—ã:
- –û–±—Ä–∞–±–æ—Ç–∞–Ω–æ 4,5% —Ç–µ—Ä—Ä–∏—Ç–æ—Ä–∏–∏ –§—Ä–∞–Ω—Ü–∏–∏.
- –ö–ª–∞—Å—Å–∏—Ñ–∏–∫–∞—Ç–æ—Ä —Å–æ–¥–µ—Ä–∂–∞–ª 133 –∫–æ–¥–∞.
- Точность векторизации в 3D — 1 м.
- –ó–∞–¥–µ–π—Å—Ç–≤–æ–≤–∞–Ω–æ 40 –æ–ø–µ—Ä–∞—Ç–æ—Ä–æ–≤.